Diversity
Diversity is always such a intereting topic in recomendation system. Everybody knows it’s important but few people really realize it in industry systems.
In this post, I will give a general introduction and also provide a detailed implementation on the most popular diversity approach DPP.
Why diversity
Ecosystem
There are many factors that show the necessity of diversity
Filter bubble. This is one of the most notorious thing people hate in recommender system which means an algorithmic bias that skews or limits the information an individual user sees on the internet. Many papers and companies want to solve this but yet there is no good answer.
User experience - Aesthetic fatigue. Tiktok is a representative here.
Data collection - limited user preference. Lack of diversity lead to homogeneous user read histories, makes machine learning models hard to capture broad preference.
Model fitting - High skewed dataset. When the popular content dominate, the training dataset will be high skewed. Means all the long-tail content maybe ignored.
Recommendation goals
From the perspective of recommendation goals, there is always a balance beween exploitation and exploration.
Exploitation
Relevant - users are likely to take actions which are shown
Transparent - it’s clear why the content selected is being recommended to the user
Contextual - the content selected is timely and relevant to a person’s profile, device and location
Adaptive - recommendation results adapt quickly to new users, new behavior and newly available content
Exploration
Coverage - new content has an opportunity to surface for a user. A significant portion of available content are recommend
Serendipitous - recommending content not obviously linked to previously expressed preferences
Diverse - Don’t show the same recommendation to a user many times in a short period. Mixture of various content type, genre or category
How to measure
There are 2 common perspectives when we look into the diversity metrics
Global view
Coverage is the main factor here, it evaluate how the user actions spread among all the content.
A simple metric can be the proportion of page view of the top items.
Personal view
Personal view defines the diversity in the current recommended items. Each time user refresh their feed, the system will deliver a new list of items. There are 2 major metrics.
Effective Catalog Size (ECS)
This metric comes from Netflix, it represent how spread viewing is across the items in our catalog.
Pi is the share of all hours streamed that came from video Vi which was the i-th most streamed video. Note that Pi≥Pi+1 for i=1,...,N−1 and
It tells us how many videos are required to account for a typical hour streamed.
For ECS, the larger the better. For example, if we only have 1 video the ECS will be 0, but if we have 2 videos and all the watching time are evenly split among these 2. The ECS will be
Diversity Index (DI)
The Gini-Simpson Index1 is also called Gini impurity.
The original Simpson index λ equals the probability that two entities taken at random from the dataset of interest (with replacement) represent the same type. Its transformation 1 − λ, therefore, equals the probability that the two entities represent different types
The gini index is consistent with ECS. The larger the more diversed content we have. And the value range is [0, 1].
Industry Practice
In a real world recommender system in industry, there are multi places we can improve the diversity.
Candidate generator
Down sample hot items, either for model or rule based CG
Multi-Interest model - MIND2, modeling multiple user interest using capsule
Exploratory model - only longtail items, the most straightforward way build a CG only provide longtail items
Ranking
Long-term interest - SIM3, also considering the long-term user interests
MTL - Long term labels, use long-term metrics as another label for multi task model
Customize utility function - PURS4, this paper modifies the utility function and take unexpectedness into consideration
Reranking
This is the most popular layer where diversity is tuned
Pointwise to Listwise, not only consider the pointwise metrics like CTR, also consider metrics for the whole list
Maximal marginal relevancy (MMR)
Determinantal point process (DPP)
Rules
We can apply different rules in or after reranking layer
Boost longtail items
Down boost hot items
Deduplicate similar items
MMR
Maximal Marginal Relevance considers the similarity of keywords/keyphrases with the document, along with the similarity of already selected keywords and keyphrases. It’s a fast greedy and popular methods. And it’s a good baseline.
Q is a query or user profile
S is the subset of documents in R already selected
R\S is the set difference, i.e, the set of as yet un-selected documents in R
Sim1 is the similarity metric used in document retrieval and relevance ranking
between documents and a query; and Sim2 can be the same as Sim1 or a different metric
λ is a tunable parameter to balance relevancy and similarity
DPP
Determinantal point process is the SOTA approach for diversity.
Youtube paper in 2018
In the youtube paper5, they
Design the serving schema, we can see the DPP layer is inserted between the ranking and policy layer
Use grid search for the naive model
Proprose a Deep DPP kernel to learn the params automatically
Hulu paper in 2018
In Hulu paper6, they propose a greedy solution for DPP.
Time complexity reduced from O(M^4) to O(M^3)
Introduce a tunable parameter θ which can balance the tradeoff between relevancy and diversity
Bring a sliding window variation
Deep dive
Let’s demystify DPP.
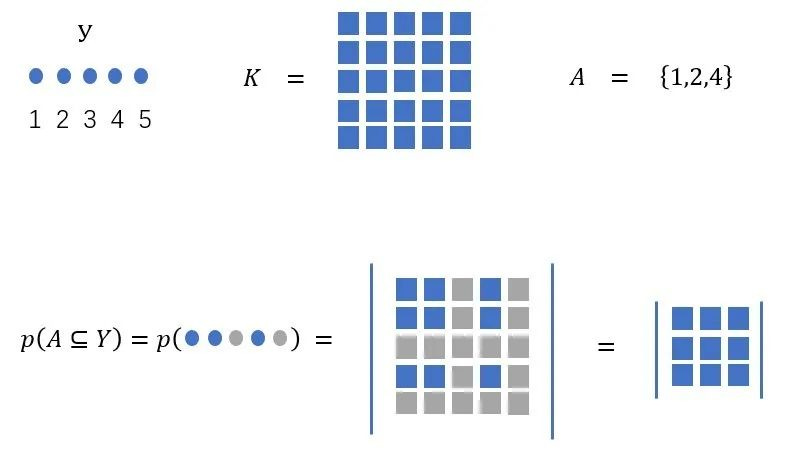
A point process is simply a probability measure on 2^y, the set of
all subsets of y
P is called a determinantal point process if, when Y is a random subset drawn according to P, we have, for every A⊆Y
We refer to K as the marginal kernel since it contains all the information needed to compute the probability of any subset A being included in Y
As we can see from the picture, what DPP do is give the probability of selecting k items from a larger pool of N items
Intuitive interpretation
If A = {i} is a singleton, then we have. Here P represents the probability of choosing i
That is, the diagonal of K gives the marginal probabilities of inclusion for individual elements of Y
If A = {i, j} is a two-element set, then
The off-diagonal elements determine the negative correlations between pairs of elements: large values of Kij imply that i and j tend not to co-occur
If we think of the entries of the marginal kernel as measurements of similarity between pairs of elements in Y, then highly similar elements are unlikely to appear together
If
then i and j are “perfectly similar”. The P will be 0 and do not appear together almost surely
This explains why DPP is “diversifying”
Intuitive geometric interpretation
L matrix can be decomposite to 2B matrix. (Such a B can always be
found for certain L)
Think of the columns of B as feature vectors describing the elements of Y
Magnitude increase -> volume increase
Similarity increase -> volume decrease
Construct kernel matrix with relevancy and similarity
ri is the relevancy scalar
fi is the normalized embedding vector
Sij is the similarity function between fi and fj
Add a log transformation
In the greedy approach, we turn it to a iterative process. Everytime pick up the i that can maximize the probability
Another variant with a tunable θ param, where α = θ/(2(1 − θ))
Algorithm implementation
The paper author provided the implementation7 in Python. But in most online serving scenario, Python is not the first choice considering the latency issue. I will provide a Java version here.
For Java implementation, I leverage a open source fast computing lib EJML8. The latency is around 20ms for 200 items while load testing.
Create the kernel matrix
Assume we already have the relevancy score which may comes from you ranking score.
For similarity scores, a general approach can be calculating the score from language models like SentenceBert or SimCSE.
/**
* Init kernel matrix
*
* @param similarity similarity scores
* @param relevancy relevancy scores
*/
private DPPAlgo(float[][] similarity, float[] relevancy) {
int itemSize = relevancy.length;
// Create diagonal matrix for relevancy
SimpleMatrix rankScoreMat = SimpleMatrix.wrap(new FMatrixRMaj(itemSize, itemSize));
for (int i = 0; i < itemSize; i++) {
rankScoreMat.set(i, i, relevancy[i]);
}
FMatrixRMaj similarityMat = new FMatrixRMaj(similarity);
SimpleMatrix simScoresMat = SimpleMatrix.wrap(similarityMat);
kernelMatrix = rankScoreMat.mult(simScoresMat).mult(rankScoreMat);
}Create the tunable version
Inject the tunable theta to the relevancy score matrix
/**
* Create a tunable DPP object
*
* @param similarity similarity scores
* @param relevancy relevancy scores
* @param theta (0, 1) larger theta favors relevancy more
*/
public static DPPAlgo CreateTunableDPPAlgo(float[][] similarity,
float[] relevancy,
double theta) {
double alpha = theta / (1 - theta) / 2;
for (int i = 0; i < relevancy.length; i++) {
relevancy[i] = (float) Math.exp(alpha * relevancy[i]);
}
return new DPPAlgo(similarity, relevancy);
}
The original version
Build the whole sequence in a loop
/**
* original version, note that the return size could be less than the required maxLength if there
* are two identical contents in terms of similarity dimension
*
* @param maxLength max result length
* @return optimized array index list
*/
public List<Integer> generateSequence(int maxLength) {
int itemSize = kernelMatrix.numRows();
SimpleMatrix cis = new SimpleMatrix(maxLength, itemSize);
SimpleMatrix di2s = kernelMatrix.diag().copy();
di2s.reshape(1, itemSize);
List<Integer> rst = new LinkedList<>();
int selectedItem = rowVectorArgMax(di2s);
rst.add(selectedItem);
while (rst.size() < maxLength) {
int k = rst.size() - 1;
double diOptimal = Math.sqrt(di2s.get(selectedItem));
SimpleMatrix elements = kernelMatrix.rows(selectedItem, selectedItem + 1);
SimpleMatrix ciOptimal = cis.rows(0, k).cols(selectedItem, selectedItem + 1);
SimpleMatrix eis = elements.minus(ciOptimal.transpose().mult(cis.rows(0, k)))
.divide(diOptimal);
cis.setRow(k, 0, eis.getDDRM().getData());
di2s = di2s.minus(eis.elementPower(2));
di2s.set(selectedItem, Double.NEGATIVE_INFINITY);
selectedItem = rowVectorArgMax(di2s);
if (di2s.get(selectedItem) < EPSILON) {
break;
}
rst.add(selectedItem);
}
return rst;
}The sliding window version
Please try to use setRow or setColumn API as many as possible to avoid unnecessary memory copy.
/**
* sliding window version, note that the return size could be less than the required maxLength if
* there are two identical contents in terms of similarity dimension
*
* @param maxLength max result length
* @param windowSize number of elements in each window
* @return optimized array index list
*/
public List<Integer> generateWindowSequence(int maxLength, int windowSize) {
int itemSize = kernelMatrix.numRows();
SimpleMatrix v = new SimpleMatrix(maxLength, maxLength);
SimpleMatrix cis = new SimpleMatrix(maxLength, itemSize);
SimpleMatrix di2s = kernelMatrix.diag().copy();
di2s.reshape(1, itemSize);
List<Integer> rst = new LinkedList<>();
int selectedItem = rowVectorArgMax(di2s);
rst.add(selectedItem);
int windowLeftIndex = 0;
while (rst.size() < maxLength) {
int k = rst.size() - 1;
SimpleMatrix ciOptimal = cis.rows(windowLeftIndex, k).cols(selectedItem, selectedItem + 1);
double diOptimal = Math.sqrt(di2s.get(selectedItem));
v.setRow(k, windowLeftIndex, ciOptimal.getDDRM().getData());
v.set(k, k, diOptimal);
SimpleMatrix elements = kernelMatrix.rows(selectedItem, selectedItem + 1);
SimpleMatrix eis = elements.minus(ciOptimal.transpose().mult(cis.rows(windowLeftIndex, k)))
.divide(diOptimal);
cis.setRow(k, 0, eis.getDDRM().getData());
di2s = di2s.minus(eis.elementPower(2));
if (rst.size() >= windowSize) {
windowLeftIndex += 1;
for (int idx = windowLeftIndex; idx < k + 1; idx++) {
double t = Math
.sqrt(Math.pow(v.get(idx, idx), 2) + Math.pow(v.get(idx, windowLeftIndex - 1), 2));
double c = t / v.get(idx, idx);
double s = v.get(idx, windowLeftIndex - 1) / v.get(idx, idx);
v.set(idx, idx, t);
v.setColumn(idx, idx + 1, v.rows(idx + 1, k + 1).cols(idx, idx + 1)
.plus(v.rows(idx + 1, k + 1).cols(windowLeftIndex - 1, windowLeftIndex).scale(s))
.divide(c)
.getDDRM()
.getData());
v.setColumn(windowLeftIndex - 1, idx + 1,
v.rows(idx + 1, k + 1).cols(windowLeftIndex - 1, windowLeftIndex).scale(c)
.minus(v.rows(idx + 1, k + 1).cols(idx, idx + 1).scale(s))
.getDDRM()
.getData());
cis.setRow(idx, 0, cis.rows(idx, idx + 1).divide(c)
.plus(cis.rows(windowLeftIndex - 1, windowLeftIndex).scale(s)).getDDRM().getData());
cis.setRow(windowLeftIndex - 1, 0, cis.rows(windowLeftIndex - 1, windowLeftIndex).scale(c)
.minus(cis.rows(idx, idx + 1).scale(s)).getDDRM().getData());
}
di2s = di2s.plus(cis.rows(windowLeftIndex - 1, windowLeftIndex).elementPower(2));
}
di2s.set(selectedItem, Double.NEGATIVE_INFINITY);
selectedItem = rowVectorArgMax(di2s);
if (di2s.get(selectedItem) < EPSILON) {
break;
}
rst.add(selectedItem);
}
return rst;
}Looks good but
By here, we cover the design and implementation details for DPP. How about the online real-world performance?
From my personal experience, although in the papers, they all claim the result is good. But sometimes it’s hard to have a perfect balance between core metrics like CTR and diversity metrics like ECS. It’s quite trivial to tune and also depends your business scenario.
That’s why we love and hate diversity at the same time.
https://en.wikipedia.org/wiki/Diversity_index#Gini%E2%80%93Simpson_index
https://arxiv.org/pdf/1904.08030v1.pdf
https://arxiv.org/pdf/2006.05639.pdf
https://arxiv.org/pdf/2106.02771.pdf
https://jgillenw.com/cikm2018.pdf
https://papers.nips.cc/paper/2018/file/dbbf603ff0e99629dda5d75b6f75f966-Paper.pdf
https://github.com/laming-chen/fast-map-dpp/blob/master/dpp.py
http://ejml.org/wiki/index.php?title=Main_Page














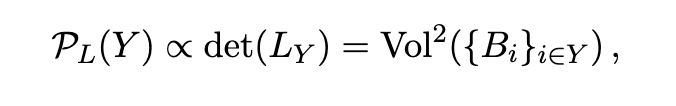




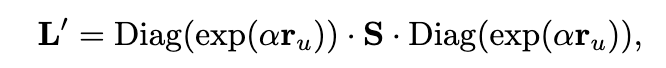



Substack's latex is so bad...