Optimization in Multi Task Learning II
Dynamic Weight Averaging, Dynamic Task Prioritization and MTL as Multi-Objective Optimization
Today let’s continue our discussion on optimization techniques in MTL. In this post, I will share the ideas and codes on the Dynamic Weight Averaging (DWA), Dynamic Task Prioritization (DTP) and MTL as Multi-Objective Optimization (MGDA/PE-LTR) methods from the survey1.
All the codes can be found in my GitHub Repo. For PyTorch version, we can refer to this MTL Repo.
Dynamic Weight Averaging
The idea of DWA is similar to GradNorm which I shared in the previous post. The target is to balance the pace at which tasks are learned. Different from GradNorm, DWA calculate the pace only based on the loss. So it doesn’t require access to gradient and there is no extra gradient descent step. The task specific weight w_i for task i at step t is:
Here N is the task number, L is the loss. And r_n represents the relative descending rate of loss L_n. T is the temperature parameter controls the softness of softmax (recall the same temperature parameter in Two-Tower model). We can see:
When the loss of a task decreases slower which means a higher r_n value, compared to other tasks, the learning weight w_i will increase.
Notice that here the weight is solely based on loss values and it only controls the loss weight other than gradient magnitude. So it requires us to balance the loss magnitudes beforehand. This is a key difference compared to GradNorm.
Code
For your reference, the code link is here. 😅 Write this code in TF is a little bit messy.
In general the code is quite similar as the GradNorm but much simpler.
Define a previous loss variable for each task to record the previous step losses
Here I use a trick to initialize the loss value for the first step. It will only overwrite the prev_loss value in the first step
Then calculate the task specific loss descending rate and weight according to the equation above
Notice that here we also need to remve the weights from tranable variables because we want to manually control it
Dynamic Task Prioritization
DTP prioritize the learning of difficult tasks by assigning them a higher learning weight. This is kind of opposite to the uncertainty weighting approach which prefer an easy task. In the survey, they think they are not necessarily conflict. And uncertainty weighting seems better suited when tasks have noisy labeled data, while DTP makes more sense when we have access to clean ground-truth annotations. In my opinion, these two approaches consider the MTL optimization task from different perspective. Uncertainty weighting cares about data quality and the noise level. DTP cares about the final metrics and task performance like AUC and accuracy. And I prefer DTP because the target of DTP is directly related to our business goal.
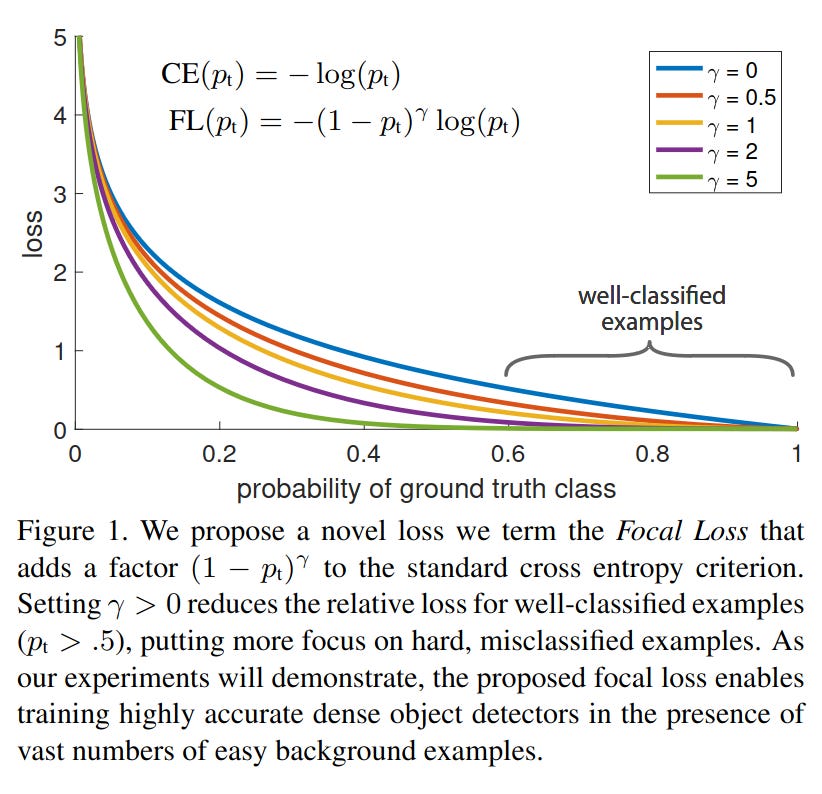
DTP borrows the idea directly from Focal loss2. Recall the Focal loss which adds a loss weight related to the prediction logits. It aims to let the model put more focus on hard and misclassified samples by decreasing the loss for easy samples and increasing the loss for hard samples.
In DTP, the loss weight is created from the key performance indicators (KPIs) which is used to quantify the difficulty of every task. The KPIs are picked to have an intuitive meaning, e.g. accuracy for classification tasks. For regression tasks, the prediction error can be thresholded to obtain a KPI that lies between 0 and 1.
DTP set the loss weight w_i for task i at step t as:
As the value for the KPI k_i increases, the weight w_i for task i is being reduced.
Similar to DWA, DTP requires to balance all the overall loss magnitude beforehand. And it also requires to carefully select the KPIs.
Code
The code link is here. Since DTP doesn’t require any calculation on the loss. It can be defined as a layer and invoked directly when building the model.
MTL as Multi-Objective Optimization
Multiple gradient descent algorithm (MGDA)3 and Pareto-Efcient algorithm with LTR (PE-LTR)4 is the most complex algorithm and it involves lots of math equations and deductions. I will only explain the basic ideas here. If you are interested in the math part, please refer to the paper for details. The methods I shared above try to solve the optimization problem by setting the task specific weights in the loss according to some heuristic. But in MGDA/PE-LTR, they take MTL as a multi objective problem with the overall goal of finding a Pareto optimal solution among all tasks.
A Pareto optimal solution is defined as: the loss for any task can be decreased without increasing the loss on any of the other tasks.
An advantage of this approach is that since the shared network weights are only updated along common directions of the task-specific gradients, conflicting gradients are avoided in the weight update step.
Code
During investigation I found PE-LTR is more widely used in industry company like Alibaba. Here is the original implementation from the paper author. I tried to re-implement it using only TensorFlow but it turned out to be too complex. So I directly import the code and using py_function to invoke it.
PE-LTR also need gradient to calculate the weight. So the implementation structure is similar to the GradNorm.
Calculate the total loss and gradient for the last shared layer. Here we borrow the idea from GradNorm
After getting the gradients, invoke the Pareto step to update the loss weights
Comparison
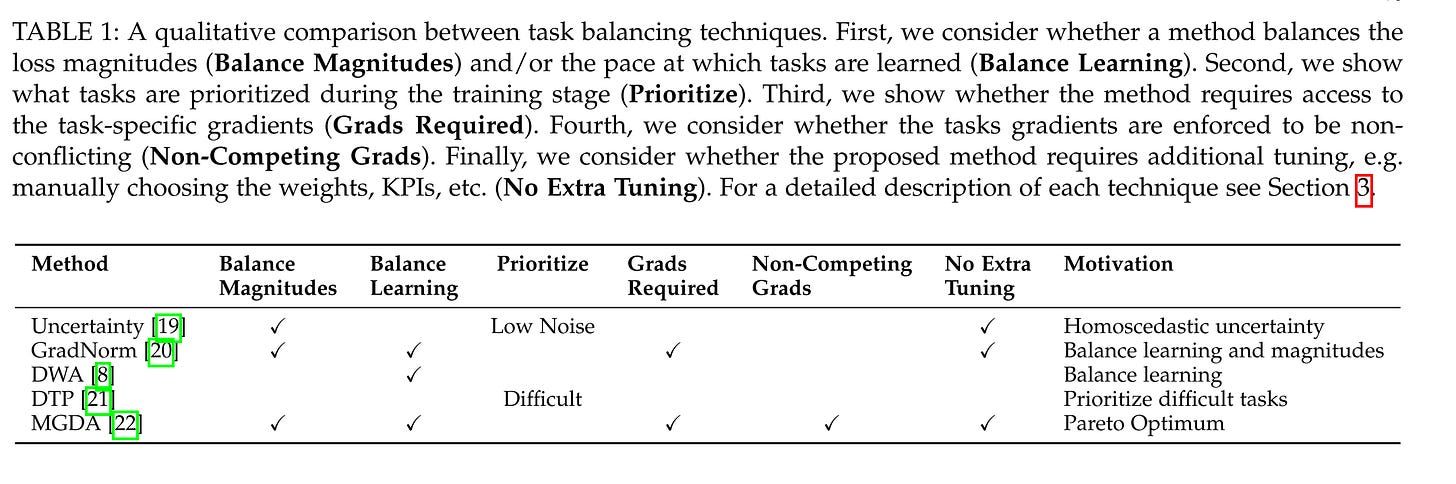
In the survey , they also provide a qualitative comparison between all the methods. From my experience, I would say all these methods are not perfect and have their pros and cons. In production, we should try and test them one by one :).
https://arxiv.org/pdf/2004.13379.pdf
https://arxiv.org/pdf/1708.02002.pdf
https://www.sciencedirect.com/science/article/pii/S1631073X12000738
http://ofey.me/papers/Pareto.pdf